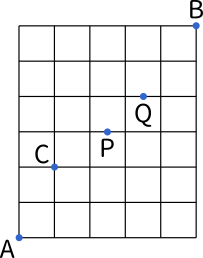
初めは、それぞれの数の倍数を書き出します。 次は、倍数を書き出したら共通の倍数を探します。 それでは、公倍数の求め方がわかりましたら、初めの作業は、2の倍数と3の倍数を書き出してみましょう。 2の倍数は、 2、4、6、8、10、12・・・ となります。応用問題には、d地点をかならず通る道順の総数、ある道が封鎖されていて通れない場合の総数などがあります。 それはまた次の機会に紹介しようと思います。 (更新) 関連記事 ・私立中学 入試対策 算数(場合の数① 碁盤目状の道順 基礎)(このページ)道順の場合の数を求める別解を解説します。「書き込み方式」などと呼ばれるものです。 点 a a a から頂点 p p p にたどりつくための最短の道順の数を n (p) n(p) n (p) と書きます。目標は n (b) n(b) n (b) を求めることです。

中学2年数学 確率 場合の数を求める問題の解き方 数学の面白いこと 役に立つことをまとめたサイト
場合の数 求め方
場合の数 求め方-場合の数と確率「同様に確からしい」の意味 場合の数と確率「条件つき確率」と「確率の乗法定理」の関係 場合の数と確率余事象を使った解き方 場合の数と確率倍数の個数の求め方 場合の数と確率区別がない組分けある場合の数が実際に現われる割合は、その場合の数を割り算で、その事柄において起こり得る全ての事柄の場合の数で割ったものに等しい。 たとえば、全く等しい割合で全ての面が出るさいころをふったときに1が出る確率は 1 6 {\displaystyle {\frac {1}{6}}} で




確率の問題の解き方 場合の数 組み合わせ と確率 現役塾講師のわかりやすい中学数学の解き方
約数の個数の求め方 まずは約数の個数の求め方を解説します。例として360で考えてみましょう。 まずは360を素因数分解します。\(360=2^3×3^2×5^1\)です。 素因数分解について詳しくはこちらの記事をご覧ください。①起こりうる全ての場合の数の集合を U、 確率を求めたい場合の数の集合を a とすると a の起こる確率 は次のように表せます。 ② 確率を求めるにあたって、 場合の数を数えるとき、抜けが無いようにするため、組合せで考えて場合を書き出し(昇順または降順で書き出す)、順列の計算をなお、税額表の甲欄を適用する場合の扶養親族等の数は、下図1を参考に求めた配偶者に係る扶 養親族等の数と、下図2を参考に求めた配偶者以外の扶養親族等の数とを合計した数となります。 《1 配偶者に係る扶養親族等の数の算定方法(具体例)》
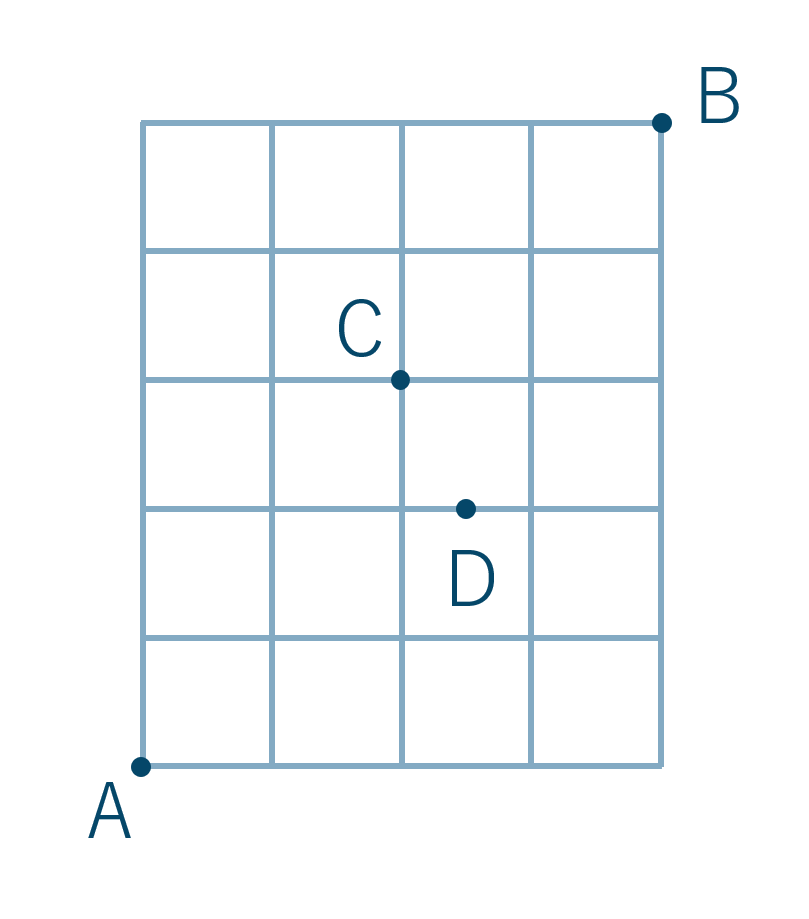
こんにちは。 da Vinch (@mathsouko_vinch)です。 約数の総和とその求め方ある自然数の約数を求めた後、その和を考えることにします。「なんで?」というツッコミは無しでお願いします(笑)。理由は"高校数学の整数の分野で 環構造(輪っかになっている場合) 以上の炭素Cの骨格があることを覚えておいてください。では、異性体の見つけ方を手順を追って説明します! 1分子式から不飽和度を求める 不飽和度とは、簡単に言うと分子の中の環の数と二重結合の数のことです。 右の図のように、道路が碁盤の目のようになった街がある。地点 a から地点 b までの長さが最短の道を行くとき、次の場合は何通りの道順があるか。(東北大)(1) 地点 c を通る。(2) 地点 p は通らない。(3) 地点 p 、および地点
11 (1,1)成分が0でなくなるように行を入れ替える。 最初から1列目の成分がすべて0の場合この操作はできないのでステップ2へすすむ。 12 1行目をc倍して (1,1)成分を1にする。 (c= (1,1)成分の逆数) 13 2行目以下に1行目の定数倍を加えて1列目の成分を2行ここでは、 エクセルで順列、組み合わせ数を算出する方法 について解説していきます。 ・エクセルで順列の計算を行う方法場合の数 ・エクセルでの重複順列の求め方 ・エクセルで組み合わせ数を求める方法 というテーマで解説していきます。場合の数と確率条件つき確率の解き方について 確率の乗法定理についてですが,全体的に意味がよくわからないんです・・・ なぜn(A∩B)が4なのかとか,その他諸々理解ができません。改めて解説してください。




算数 場合の数の解き方は 問題別に考え方を解説 数スタ




順列と組み合わせの違いとは そしてそれぞれの意味を0から解説
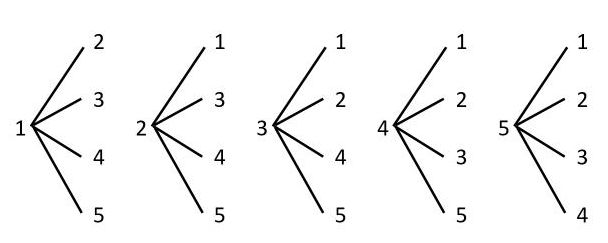
男子5人, 女子3人が一列に並ぶとき, 男子が両端になる並び方は何通りあるか求めよ。 解答 この問題は順番が関係あるので順列 両端の男子の選び方は ←条件処理 5 p 2 = この間に、残りの6人を並べるので 6 p 6 =6!=7 よって、求める場合の数は 目次 1 数学 質問解答 場合の数硬貨で払える金額の「場合の数」の考え方・解き方はこちらです数a 高校数学(質問ありがとうございました! 11 具体例を、いくつか考えて、規則や傾向を考える;場合の数の求め方の指導の段階で、生徒が最初につまずくのは組合せの考え方である。 教科書通りに展開していけば、組合せは順列の後の指導となるが、組合せの個数をx通りとして、 x×r!= n P r から組合せを間接的に考える。 こういう考え方は数学的




高校数学無料問題集 数a 第1章 場合の数と確率 確率の計算 桝 ます Note




場合の数と確率を総まとめ 各種公式 重要記事一覧 受験辞典
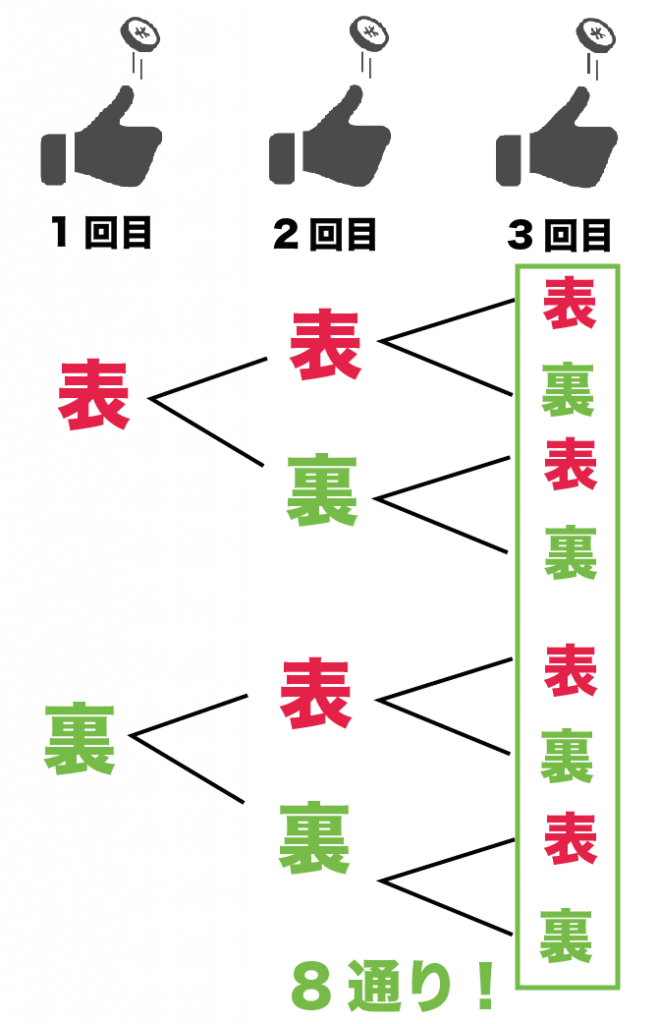
慣れてきたら、 2進数のまま計算する方法② を使ってみましょう。 「1 1 = 0」「1 0 = 1」のように 1から 引く際は問題ありませんが、「0 1」のように 0から1を引く 際は 上の位から数字を借りてきます 。 10進数の引き算と同じ要領ですね。 1つ上の位にも借りてくる数字がない場合(数字が0の この2種類の問題では、それぞれ答えが変わってきます。 ①は 順列 で、答えは 5 P 2 =5×4=通り ②は 組み合わせ で、答えは 5 C 2 =5×4÷2=10通りになります。くじの出方の全体の場合の数は N=5 当たりくじが出る場合の数は n=2 どのくじの出方も「同様に確からしい」から,確率は p= 確率は, すなわち,(部分の数)÷(全体の数)で求められるが,




完全順列の課題1と課題2が分かりません Clear



上何 通り ある か 計算 小学生 子供のための最高のぬりえ
場合の数と確率 56 数学Aサイコロの最大値が5、最小値が2になる確率はどうやって考える? 場合の数と確率 427パーセントの意味を図解で分かりやすく解説 「パーセント」というのは「百分率」で求められる単位です。 では「百分率」とは何かと言うと、全体を "100" とした時に、対象のものがどれくらいなのかを表します。 少し違う言い方をすると、『全体を100個に分けた時、対象のものはいくつか? となり、対角線の長さacが求められました。 多角形の対角線の本数の求め方 多角形の対角線の本数は、いちいち引いて数えなくても公式を使って一瞬で求められます。 対角線の本数=(頂点の数)×(頂点の数−3)÷2 という公式が存在するのです。




無料 中2数学 基本解説 解答プリント 236 確率4 求め方2



Www Tochigi Edu Ed Jp Center Cyosa Cyosakenkyu Kyokasido H21 Sugaku 03 Pdf
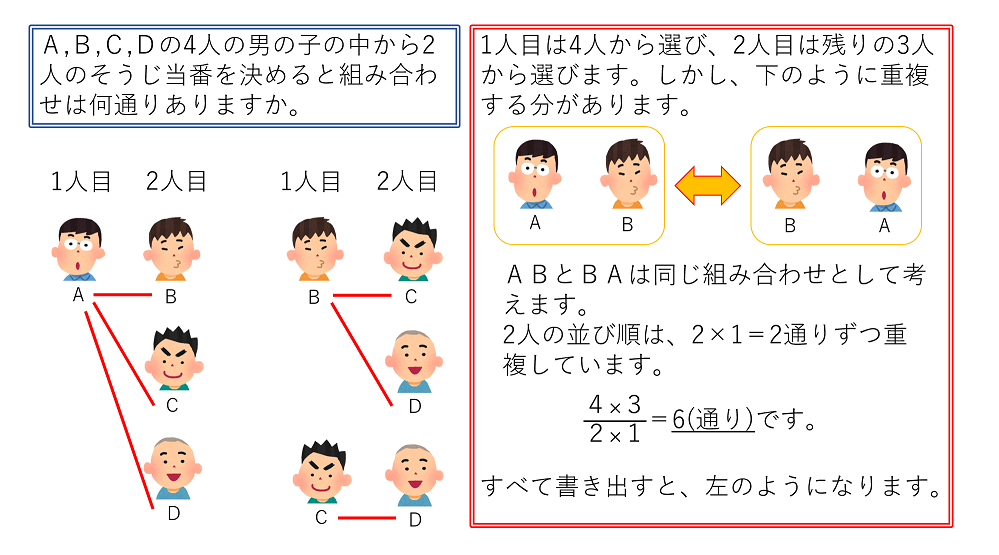
よって限定100枚に対して予約数は01倍(100分の10倍)ということが分かります。 図にしてみると以下の通りです。 限定100枚のtシャツに対し、予約数が1枚の時 では限定100枚のtシャツ(全体の量)に対し、予約数1枚(比べる量)の場合は何倍なのか?場合の数と確率倍数の個数の求め方 倍数の個数の求め方 どうやったら1から100までの整数のうち, 3の倍数や5の倍数でないのかを導きだせるのかよくわからないです。 そのため、\(n\) 個のうちの \(1\) 個の位置を固定して 場合の数を考えます。 例えば、A、B、C の \(3\) 人を円形に並べる場合、A の位置を固定してあげると、あとは B、C の \(\bf{2}\) 人の並び方だけを考えればいいのです。 したがって、求める場合の数は




高校数学 場合の数 積の法則とは 数樂管理人のブログ



解き方解説 場合の数を計算で解く 場合の数は計算でサボれ
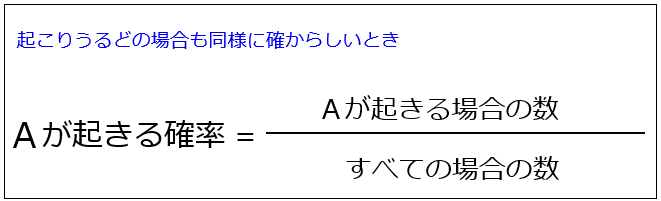
ここでの内容は、こんな人に向けて書いています 「場合の数」って何? 中学数学の場合の数を求める問題の解き方をわかりやすく教えてほしい このページでは、「場合の数」について丁寧な解説を行っていきます。 場合の数は、中学数学の確率の単元で一番はじめに登場しますね。 そし確率の求め方とは?全体分の求める数です まず、確率における基本中の基本を $2$ つまとめておきます。 確率とは何か → 確からしさの度合い。事象の起こりやすさ。 確率の求め方 → $\displaystyle \frac{問われている事象の場合の数}{全事象の場合の数}$以上より,点 p と×を通る場合は (通り) となるので,点 p を通り×を通らない最短経路は, (2) で求めた点 p を通る総数からこれを引いて (通り) となります。「~しない場合の数」を求める場合,最後に引くことを忘れないよう注意しましょう。



場合の数と確率の基礎を解説 受験に役立つ樹形図 数え上げのコツ Studyplus スタディプラス




何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ
場合の数の考え方 場合の数は制限の強い順から考える! 制限の強い順と言っても分からないと思うので、次の問題を通して説明をしたいと思い ます。 問題2 0~5までの6つの整数から異なる3個を使って3ケタの整数をつくる。 (1) 全部で何個できるか ここでの内容は、こんな人に向けて書いています 「場合の数ってなに?」という人 「求める方法はどんなものがあるの?」という人 「場合の数と確率はどんな関係?」という人 確率を学ぶには、必ず場合の数を学ぶ必要があります。 ここでは、そんな重要な場合の数について学んでいき




3分で分かる 約数の個数 約数の総和の求め方 公式をわかりやすく 練習問題付き 合格サプリ




高校数学a 最短の道順の求め方 映像授業のtry It トライイット




確率の問題を間違えてしまう5つの原因と求め方とは 高校生向け受験応援メディア 受験のミカタ




中2 確率 まとめ 中学生 数学のノート Clear



Q Tbn And9gcqk 07pns6gblxpztbesi Hjq Rmi0dl3bcobqphecjrlms6b O Usqp Cau




最短経路問題の応用 池がある場合 の解き方とは わかりやすく解説 遊ぶ数学



確率計算の公式から 確率の求め方の苦手ポイント 同様に確からしい を武器に変える記事 アタリマエ




条件付き確率の公式と求め方を分かりやすく解説




苦手な人向け 順列pの計算のやり方を簡単にサクッと解説するぞ 数スタ




余事象を利用した場合の数の求め方 数学の偏差値を上げて合格を目指す



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




場合の数47 ベル数 怜悧玲瓏 高校数学を天空から俯瞰する



解き方解説 場合の数を計算で解く 場合の数は計算でサボれ




スタディピア 場合の数と確率




場合の数と確率 数スタ



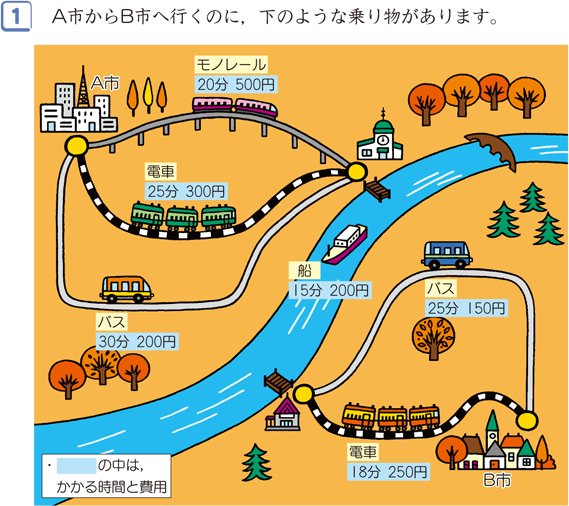
1



数a場合の数 最短経路の求め方 どうしてcを使うの Mm参考書




高校数学a 集合 の要素の個数 映像授業のtry It トライイット



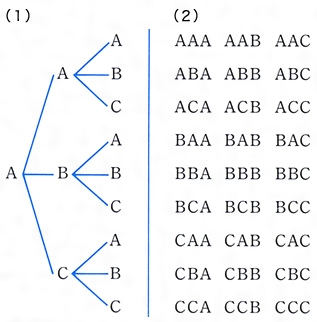
3




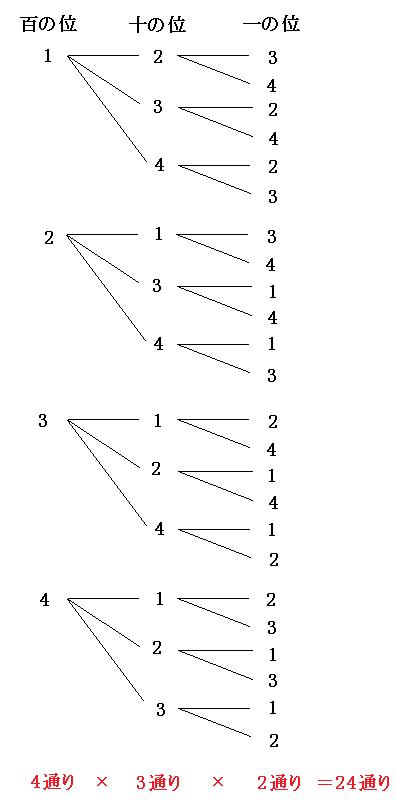
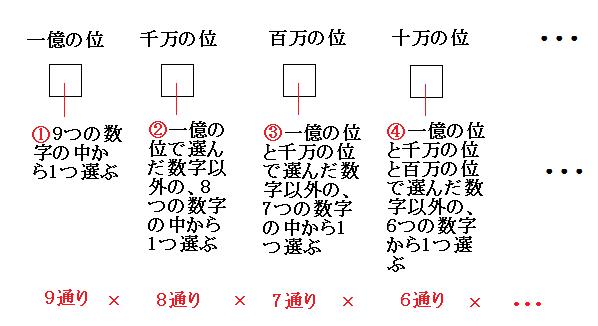
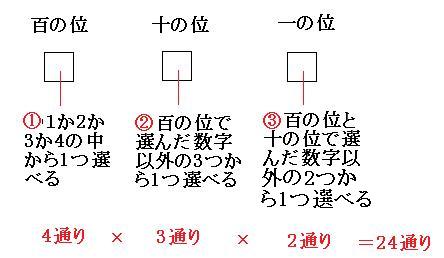
N桁の数を作る場合の数の求め方 条件が厳しい所から決めて行く




中学2年数学 確率 場合の数が分かれば確率が分かる 数学の面白いこと 役に立つことをまとめたサイト



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ




中学2年数学 確率 確率の求め方 たった1つの公式ですべてわかる 数学の面白いこと 役に立つことをまとめたサイト




中学数学 場合の数がわかる2つの調べ方 Qikeru 学びを楽しくわかりやすく




この問題全体の考察を書かなければならないのですが 全く思いつかないので考えてほしいで Clear



積の法則 和の法則とは 違いや問題の解き方をわかりやすく解説 受験辞典



中学数学 確率の求め方がわかる1つの公式 計算式 Qikeru 学びを楽しくわかりやすく



場合の数1 数え上げの原則 怜悧玲瓏 高校数学を天空から俯瞰する




中学数学 場合の数がわかる2つの調べ方 Qikeru 学びを楽しくわかりやすく




数学a 展開したときの項の数を求め方は 数スタ
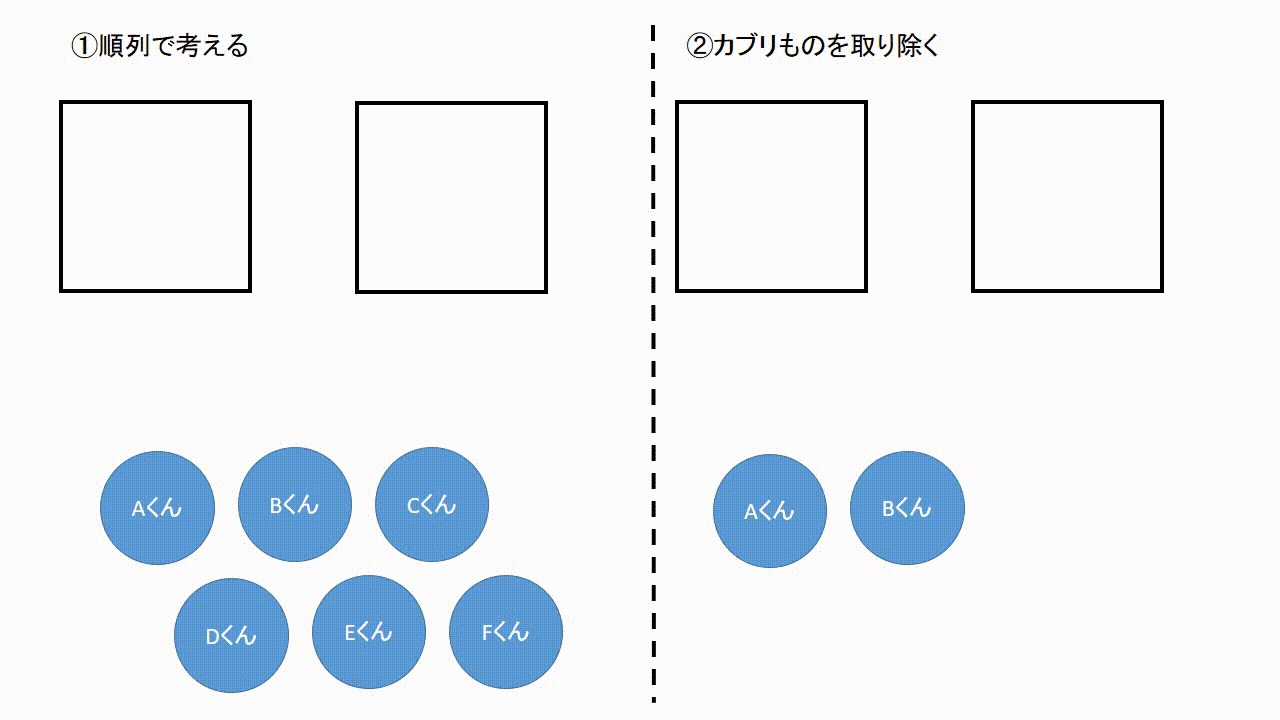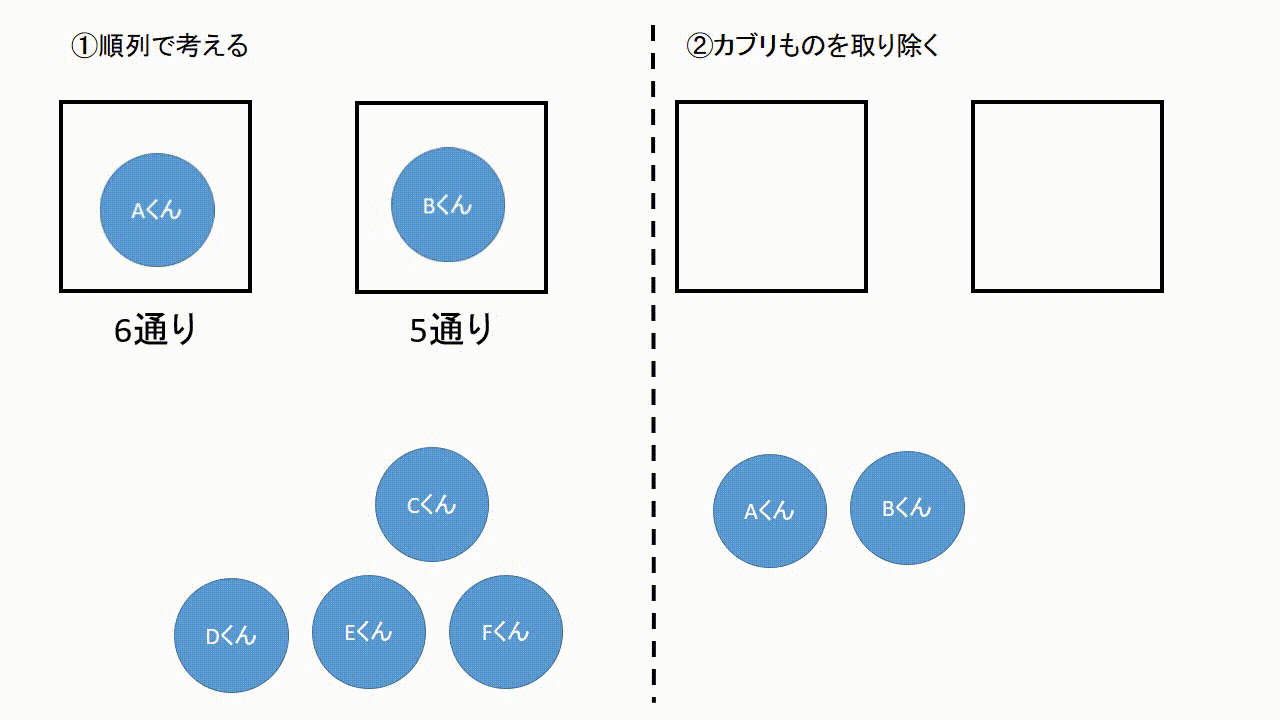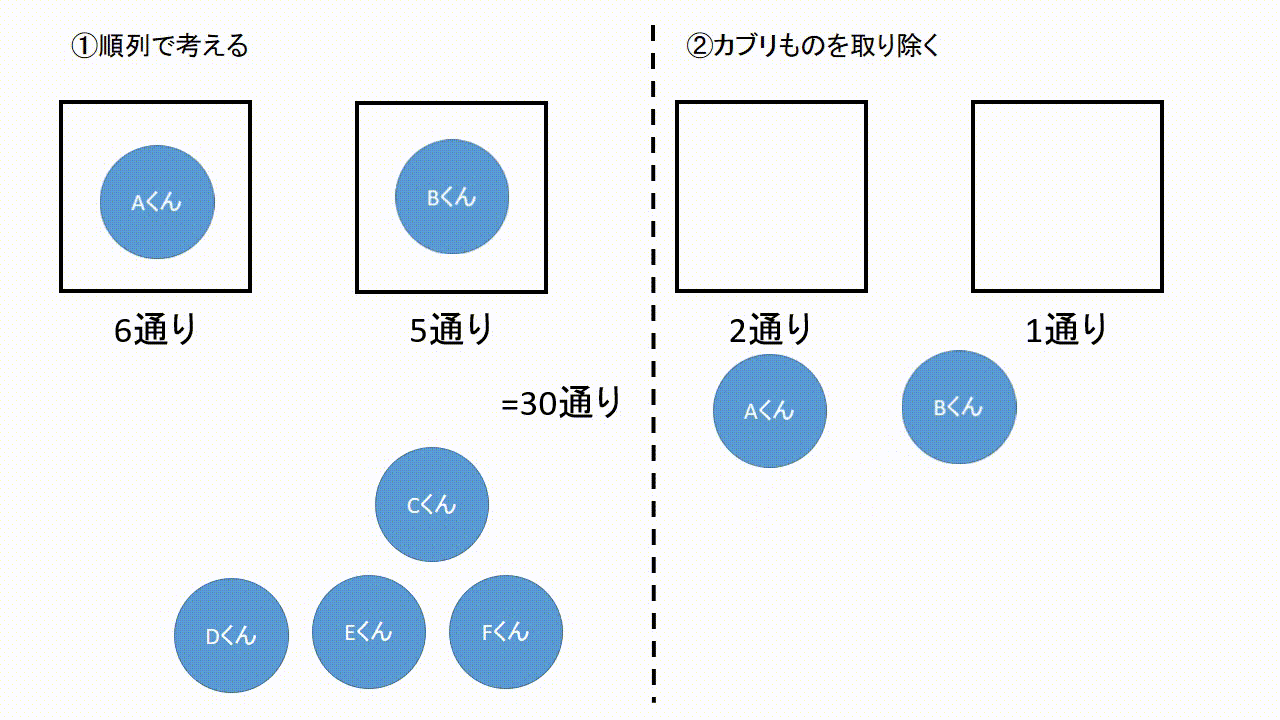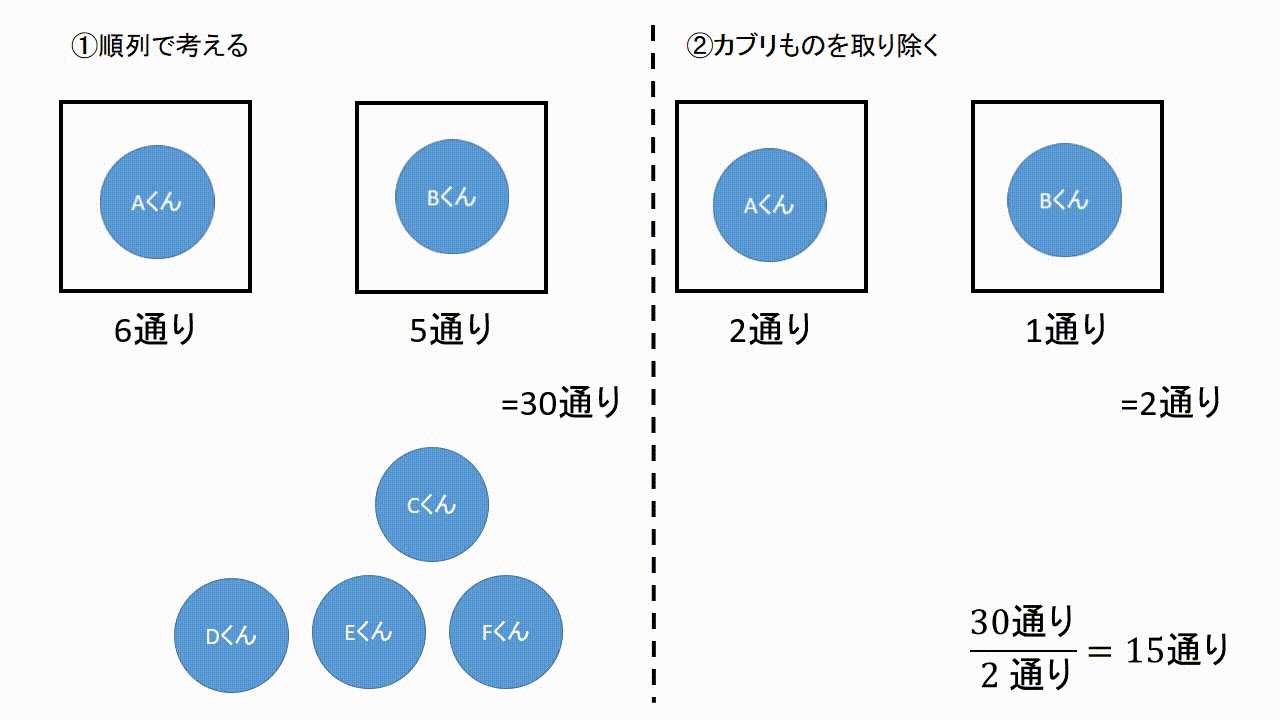



数学 確率を極めるには 場合の数 を極めろ




組み合わせncrはどう計算する 求め方から性質までを攻略



解き方解説 場合の数を計算で解く 場合の数は計算でサボれ




高校数学a A B の要素の個数 練習編 映像授業のtry It トライイット




高校数a 場合の数 Cの計算方法 オンライン無料塾 ターンナップ Youtube




2講 場合の数 1章 場合の数と確率 問題集 高校数学a



教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学



場合の数と確率を総まとめ 各種公式 重要記事一覧 受験辞典




U9 9n305vcpu M



高校一年生の数学aの教科書の場合の数と確率という単元の組み分けの問題です Yahoo 知恵袋




正負の数の利用 平均を求める Youtube



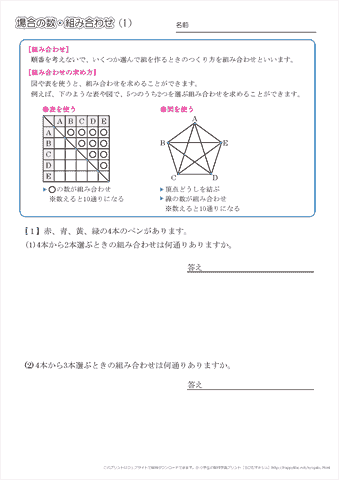
数学a 組み分けの場合の数の求め方 考え方をイチから解説 数スタ




高校数学a 場合の数 の数え方2 積の法則 例題編 映像授業のtry It トライイット




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




場合の数基礎1 和の法則 積の法則大事な2パターン 高校生向け受験応援メディア 受験のミカタ



小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




中学2年数学 確率 場合の数を求める問題の解き方 数学の面白いこと 役に立つことをまとめたサイト




場合の数 場合の数について 日々是鍛錬 ひびこれたんれん




無料 中2数学 基本解説 問題プリント 235 確率3 意味 求め方1




高校数学a 場合の数とは 映像授業のtry It トライイット




確率の問題の解き方 場合の数 組み合わせ と確率 現役塾講師のわかりやすい中学数学の解き方




場合の数27 第2種スターリング数5 漸化式の証明 怜悧玲瓏 高校数学を天空から俯瞰する



場合の数 算数用語集




中学2年数学 確率 場合の数が分かれば確率が分かる 数学の面白いこと 役に立つことをまとめたサイト




中学数学 場合の数がわかる2つの調べ方 Qikeru 学びを楽しくわかりやすく



場合の数とは コトバンク




約数の個数と総和を求める公式と なぜそのような公式になるのかを解説 ますますmathが好きになる 魔法の数学ノート



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ




場合の数 並べる と 選ぶ の計算方法の違い




数学 質問回答 約数の個数と 約数の総和の求め方 高校数学 集合 場合の数 質問ありがとうございました 行間 ぎょうのあいだ 先生



場合の数 学び家 Com




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ



数学言語としての場合の数の求め方




オリジナルの高校数学の問題を掲載していきます P 場合の数 確率




場合の数の求め方 数学ブック 7 杉村 保 本 通販 Amazon




解き方解説 場合の数を計算で解く 場合の数は計算でサボれ




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




場合の数 並べる と 選ぶ の計算方法の違い




高校数学 数a 5 場合の数 正の約数編 Youtube




確率の問題を間違えてしまう5つの原因と求め方とは 高校生向け受験応援メディア 受験のミカタ




場合の数28 第2種スターリング数6 表の活用 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学a 場合の数 の数え方2 積の法則 例題編 映像授業のtry It トライイット




高校数学a 確率の定義 場合の数との違い 同様に確からしい とは 受験の月
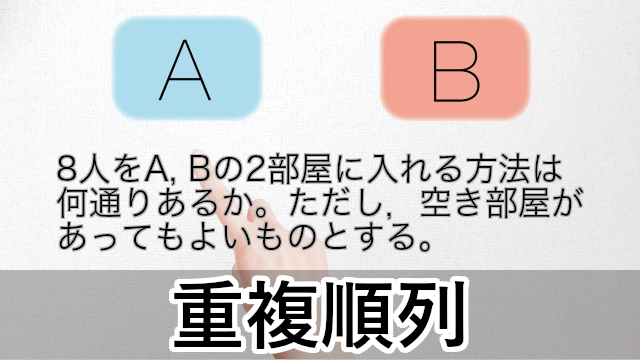



数学ia 重複順列の場合の数の求め方 大学入試数学の考え方と解法




場合の数 場合の数について 日々是鍛錬 ひびこれたんれん




倍数の個数の求め方 数学 苦手解決q A 進研ゼミ高校講座
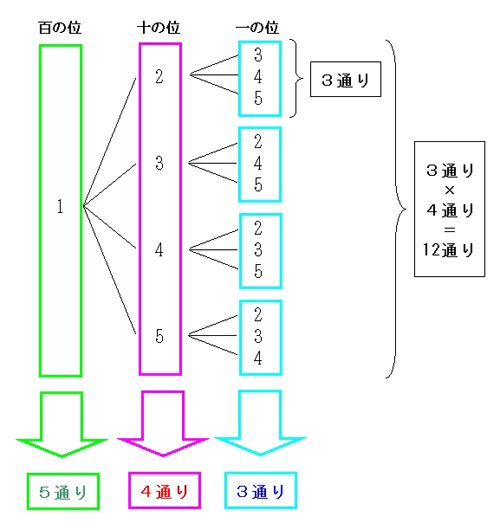



場合の数
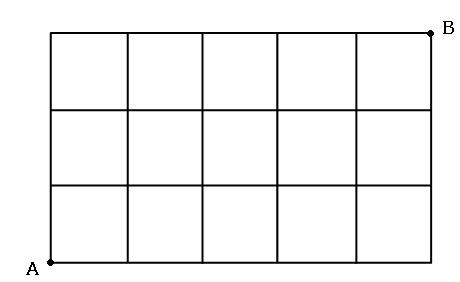



道順を求める場合の数の裏技 場合の数の道順は数字を書きこんでいけ




場合の数 組み合わせの計算方法について 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開
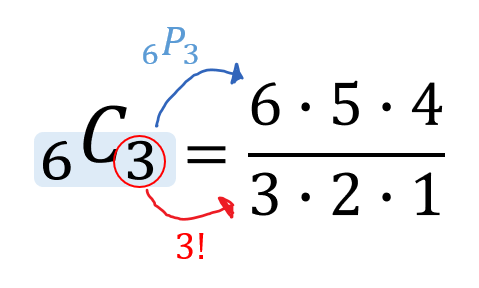



苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
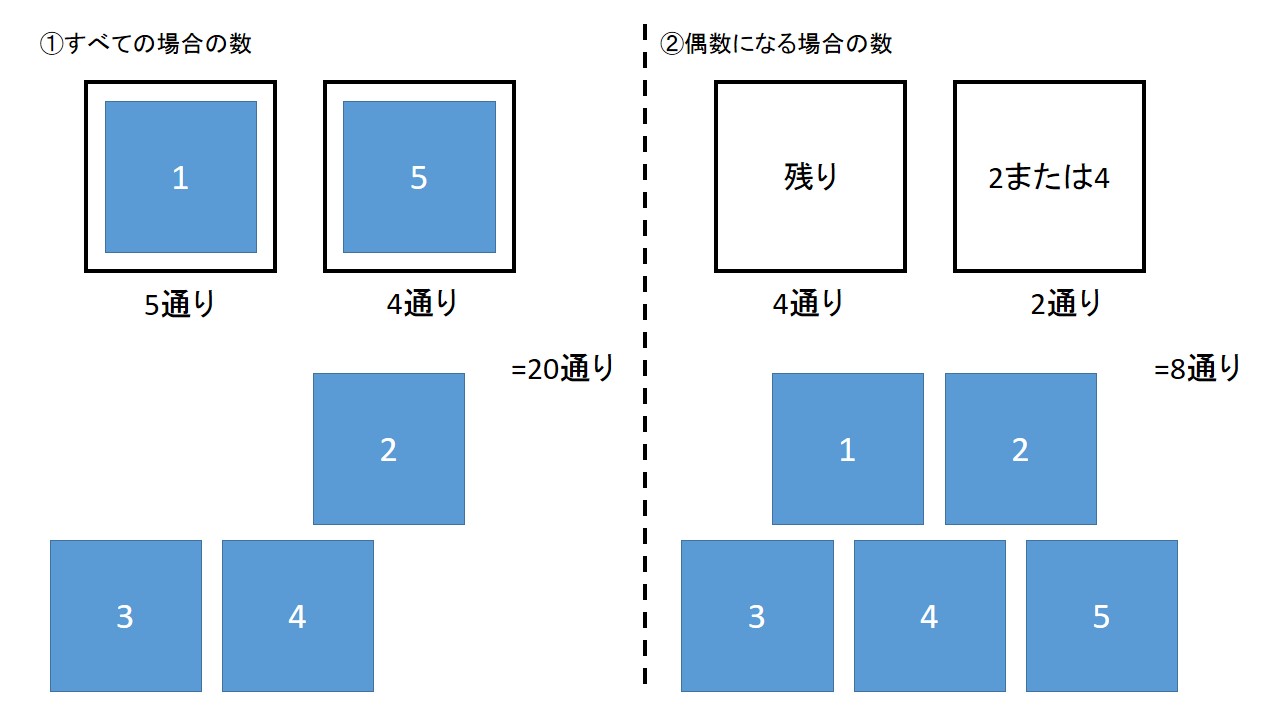



数学 確率を極めるには 場合の数 を極めろ




サイコロの確率の計算問題13選 2つ投げる場合の求め方とは 遊ぶ数学




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート



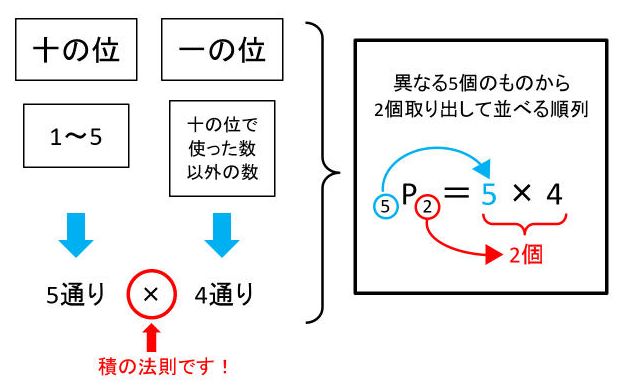
3




算数 場合の数の解き方は 問題別に考え方を解説 数スタ




場合の数と確率 の勉強法のわからないを5分で解決 映像授業のtry It トライイット




高校 数学a 場合の数33 最短の道順 13分 Youtube




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ




円順列の公式と求め方を分かりやすく解説 なぜ円順列は1



0 件のコメント:
コメントを投稿